背景

我们知道，使用前缀和可以快速求原数组一段的和。O(1) 但是如果要修改原数组中某个数，前缀和数组需要重新构建。O(n)

如果只使用数组，那么求数组中一段的和就需要遍历。O(n) 我们发现”鱼与熊掌不可得兼“了。

树状数组

引入

树状数组可以将两个操作都实现到log级别。

操作	数组	前缀和数组	树状数组
求前缀和	O(n)	O(1)	O(logn)
修改值	O(1)	O(n)	O(logn)

考虑倍增思想。 计算前7个数的和，可以拆分成长度为4 + 2 + 1的区间。[1, 4] + [5, 6] + [7] 计算前5个数的和，可以拆分成长度为4 + 1的区间。[1, 4], [5] 我们会发现有些区间和，比如[1, 4]是可以复用的。 诶？我们就用t数组来表示区间和。 t[4] = sum[1, 4] t[5] = a[5] t[6] = sum[5, 6] t[7] = a[7] 会发现求任意前缀和，其实都是可以由这些类似的小区间拼合的。 那么t[x]一定是以a[x]结尾的区间和，长度呢？就是lowbit(x)。

这个t其实就是树状数组了，我们来看下结构：

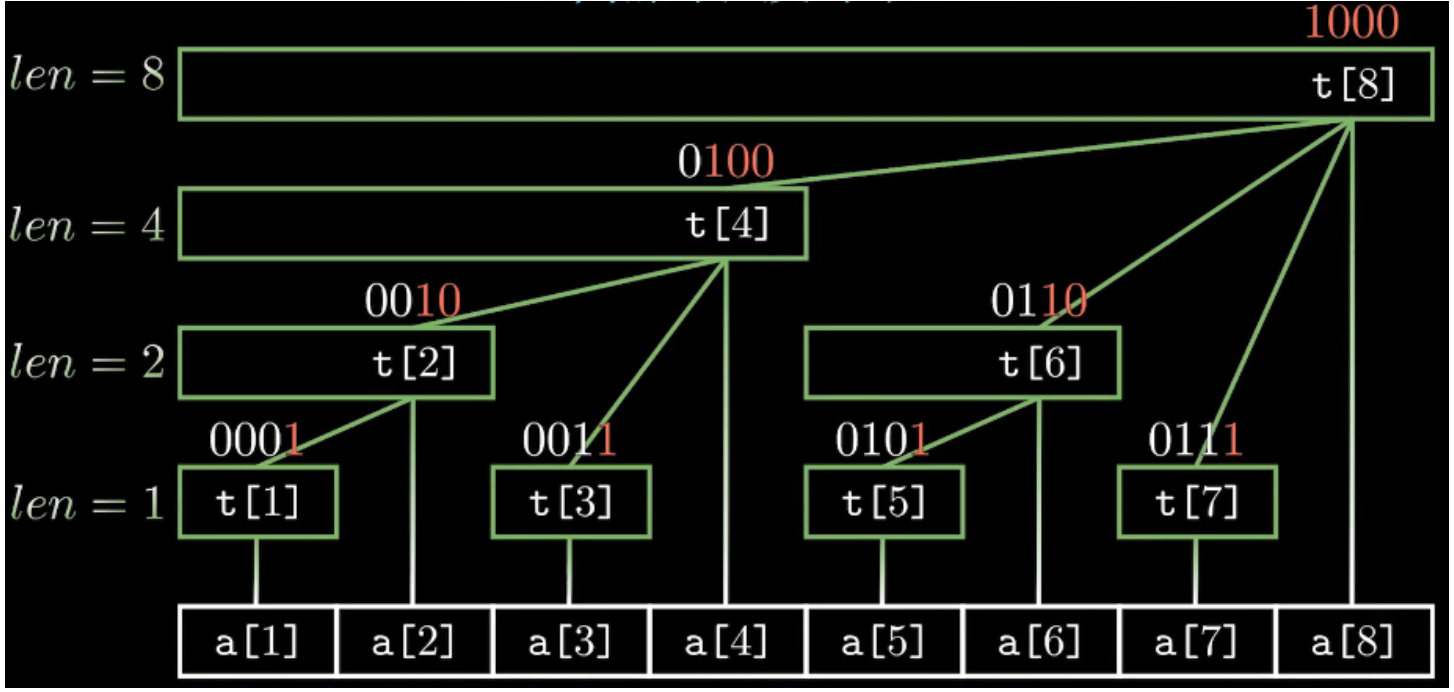
这个数组长得类似一个树形结构。

关于lowbit可查看： C++中的位运算 (opens new window)

修改操作 add(x, k)

add(x, k)表示给a[i] += k; add(3, k)举例如下。

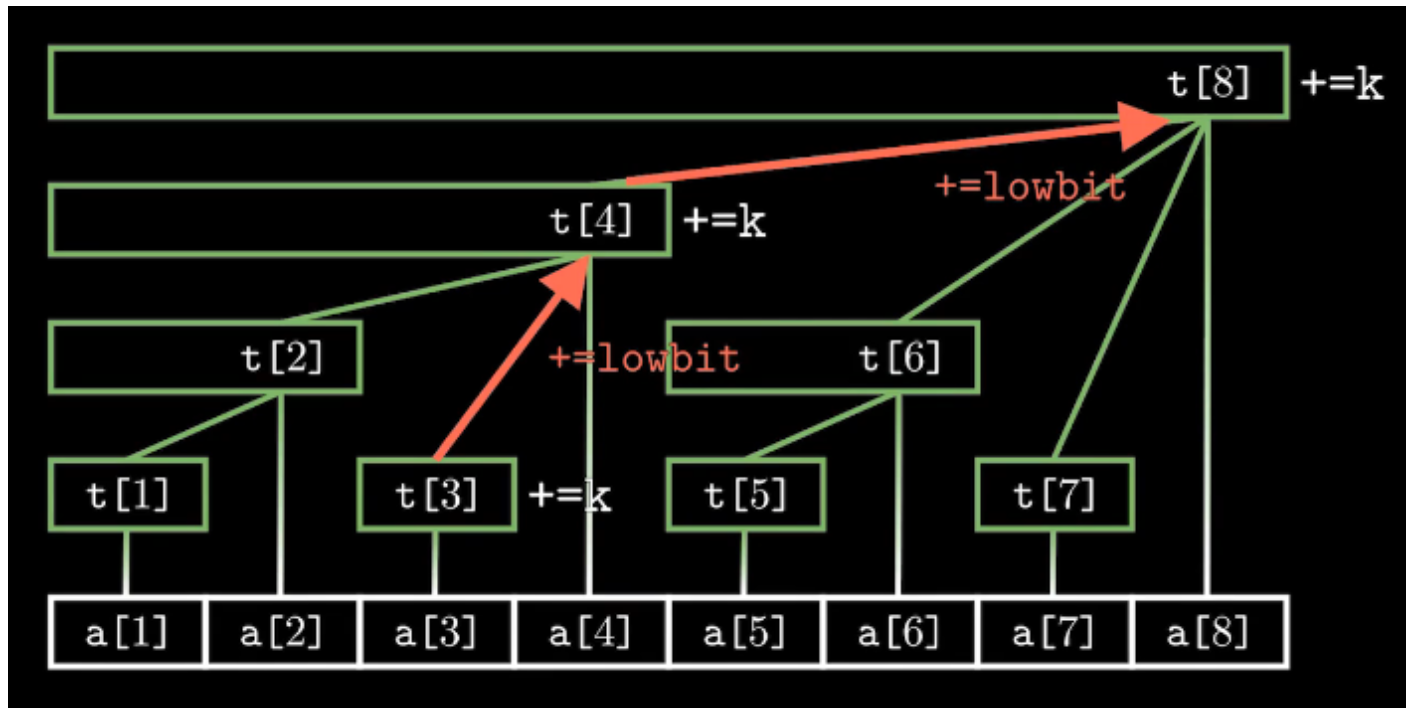
修改时，我们只需要找到包含a[3]的子数组，将其增加k即可。通过+lowbit(i)就可以找到包含关系中的父节点。

void add(int x, int k) {
    for (int i = x; i <= n; i += lowbit(i)) t[i] += k;
}

查询操作 ask(x)

ask(x)表示求前x个数的和。ask(7)举例如下。

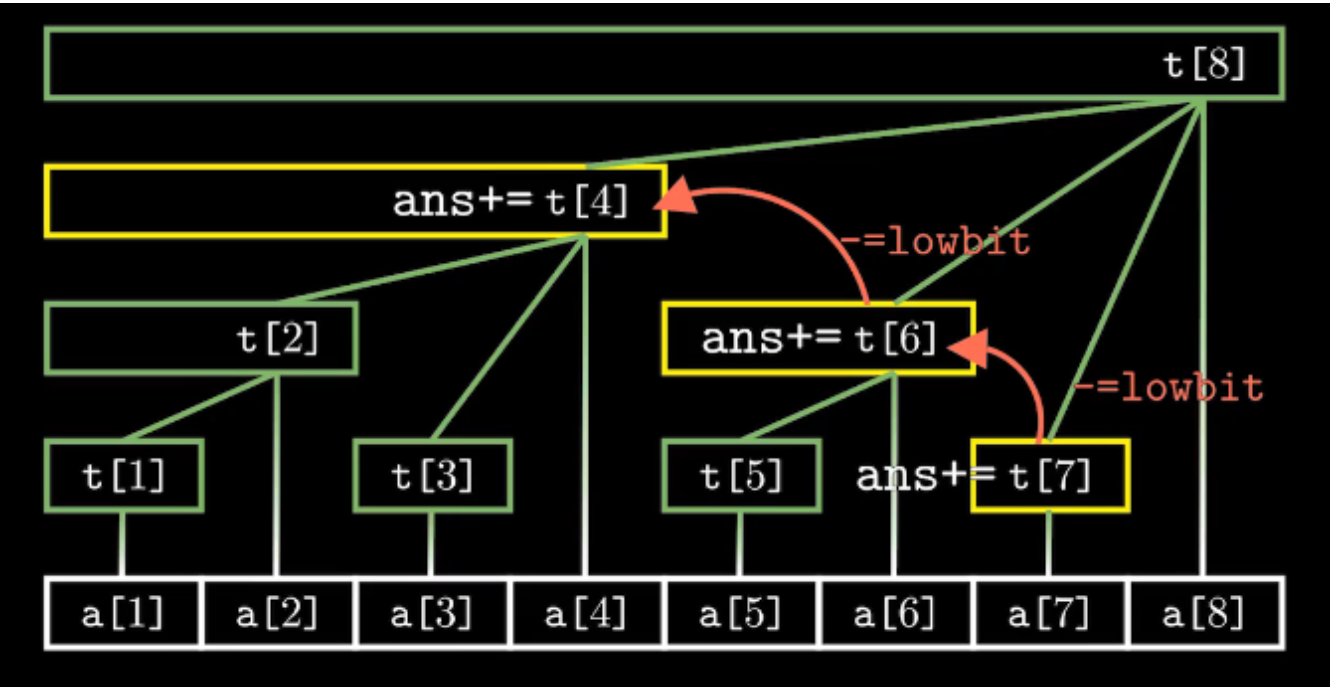
查询时，我们可以从t[7]开始，通过-lowbit(i)逐级找到前面的子区间。

int ask(int x) {
    int sum = 0;
    for (int i = x; i; i -= lowbit(i)) sum += t[i];
    return sum;
}

例题

模板-树状数组1 (opens new window)

#include <bits/stdc++.h>
using namespace std;

const int N = 500005;
int n, m;
int t[N]; // 不需要原数组a[i]

int lowbit(int x) {
    return x & -x;
}

int ask(int x) {  // 求1->x的和  s[7] = t[7] + t[6] + t[4]
    int sum = 0;
    for (int i = x; i; i -= lowbit(i)) sum += t[i];
    return sum;
}

void add(int x, int k) { // 对a[x] + k的操作
    for (int i = x; i <= n; i += lowbit(i)) t[i] += k;
}

int main(void) {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        int t;
        cin >> t;
        add(i, t); // 更新到树状数组里面了
    }

    while (m--) {
        int op;    // 读入运算 1 or 2
        cin >> op;
        if (op == 1) {
            int x, k;
            cin >> x >> k;
            add(x, k);
        } else if (op == 2) {
            int x, y;
            cin >> x >> y;
            cout << ask(y) - ask(x - 1) << endl;
        }
    }
    
    return 0;
}

模板-树状数组2 (opens new window)

此题存差分即可。 改原数组区间 => 对差分数组修改两端点 求原数组第x个数 => 对差分数组求前x个数的和

#include <bits/stdc++.h>
using namespace std;

const int N = 500005;
int n, m;
int t[N];

int lowbit(int x) {
    return x & -x;
}

void add(int x, int k) {
    for (int i = x; i <= n; i+=lowbit(i)) t[i] += k;
}

int ask(int x) {
    int res = 0;
    for (int i = x; i; i-=lowbit(i)) res += t[i];
    return res;
}

int main(void) {
    cin >> n >> m;
    int last = 0;
    for (int i = 1; i <= n; i++) {
        int t;
        cin >> t;
        add(i, t - last);
        last = t;
    }

    while (m--) {
        int op;
        cin >> op;
        if (op == 1) {
            int x, y, k;
            cin >> x >> y >> k;
            add(x, k);
            add(y + 1, -k);
        } else if (op == 2) {
            int x;
            cin >> x;
            cout << ask(x) << endl;    
        }
    }

    return 0;
}

HairCut (opens new window)

树状数组求逆序对。数组中存某个数出现的个数。 从左向右遍历，查找左侧 比当前数大的 数的个数 即可。

这道题可以理解成”生发“过程，而不是”脱发“过程。 思考一下，头发从0长到1的过程中，会产生的逆序对的数量，其实就是0左侧比0大的数的个数。 样例举例：

0 0 0 0 0
1 1 1 1 0 => 头发长到1的过程，产生了4对逆序对，也就是原数组中0左侧比0大的数的个数。

所以我们开一个s[x]存x左侧比x大的数。 随着头发的”生长“，输出答案即可。

由于本题中头发长度可能为0，会导致add函数死循环，所以我们将所有调用add，ask的位置，角标都增加1。

要注意N最多是，逆序对数量可能会超过int表达范围。所以和逆序对计算相关的s数组以及ans变量，我们用ll表示。

#include <bits/stdc++.h>
using namespace std;

const int N = 100005;
typedef long long ll;
int n;
int t[N];
ll s[N];  // s[x]:x左侧比x大的数有多少个 s[3]

int lowbit(int x) {
    return x & -x;
}

void add(int x, int k) {
    for (int i = x; i <= n + 1; i += lowbit(i)) t[i] += k;
}

int ask(int x) {
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) res += t[i];
    return res;
}

int main(void) {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        int t;
        cin >> t;
        add(t + 1, 1);  // t出现的次数+1
        s[t] += ask(n + 1) - ask(t + 1); // [t + 1, n]这些数出现了多少次
    }

    ll ans = 0;
    for (int i = 0; i < n; i++) {
        cout << ans << endl;
        ans += s[i];
    }
    return 0;
}

牛为啥过马路 III G (opens new window)

区间类问题，经常会用到贪心的思路。 样例对应的数列为[3, 2, 4, 4, 1, 3, 2, 1]，会发现数3和数2，数1和数2，数1和数3的范围有交叉。答案即为3对。 我们可以按照每个数的覆盖范围从大到小排个序。 数3对应的范围是[1, 6] 数2对应的范围是[2, 7] 数1对应的范围是[5, 8] 数4对应的范围是[3, 4] 在从长到短遍历区间的过程中，我们会发现，当前区间A若包含已遍历区间B的端点，则A、B一定存在交集。

我们需要在遍历的过程中，记录区间端点x出现的次数a[x]。 同时，我们当前遍历到的区间[l, r]与已遍历区间所能构成的答案数为sum(a[l + r, r - 1])。

发现a数组既要单点修改，又要求区间和。用树状数组实现。

#include <bits/stdc++.h>
using namespace std;
const int N = 50005;
int n;
int t[2 * N];   // 树状数组
struct segment{  // 记录每个数左右端点的位置v
    int l, r;
}s[N];
int lowbit(int x){   // lowbit函数
    return x & -x;
}
void add(int x, int k){  // 单点加法
    for(int i = x; i <= 2 * n; i+= lowbit(i)){
        t[i] += k;
    }
}
int ask(int x){   // 求前x个数的和
    int ans = 0;
    for(int i = x; i; i -= lowbit(i)){
        ans += t[i];
    }
    return ans;
}
bool cmp(segment s1, segment s2){  // 自定义比较函数
    return s1.r - s1.l > s2.r - s2.l;
}
int main(void) {
    scanf("%d", &n);  // 区间的个数
    for(int i = 1; i <= 2 * n; i++){
        int a;
        scanf("%d", &a);  // a是数, i是位置
        if(s[a].l) s[a].r = i;  // l[a]: 左边界已存在, 改右边界
        else s[a].l = i;
    }
    sort(s + 1, s + n + 1, cmp);  // 将所有区间从大到小排好序
    int ans = 0;  // 记录交叉的次数
    for(int i = 1; i <= n; i++){  // 从长到短扫描区间
        ans += ask(s[i].r - 1) - ask(s[i].l);
        add(s[i].l, 1);
        add(s[i].r, 1);
    }
    printf("%d", ans);
    return 0;
}