背景

前缀和与差分技巧都体现了预处理思想，它们互为逆运算。本篇讲解一维前缀和与差分的知识要点。 ！代码不做说明，则数组角标从1开始。

前缀和

问题背景

给定一个长度为n的数组，给m次询问，每次询问求出从下标l到下标r的数之和。

暴力方法

对于每一次询问，我们都用一个for循环去计算从下标l到下标r之间所有数的和。

int ans = 0;
for (int i = l; i <= r; i++) {
    ans += a[i];
}

时间复杂度分析

一共m次询问，每次最多要遍历长度为n的数组，时间复杂度为。

前缀和方法

我们引入前缀和数组s，s[i]则表示数组中前i项的和。 构建一维前缀和数组的方式：s[i]=s[i-1]+a[i]，前i个数的和是前i-1个数的和加上第i个数。

a 1 2 3 4  5
s 1 3 6 10 15

我们想求第2个数到第4个数的和，我们可以用s[4]-s[1]，前4个数的和减去前1个数的和，就是区间[2, 4]的和。 有了前缀和，计算区间和就不再需要for循环遍历一遍了，可以直接通过前缀和数组端点作差得到。

a[l, r] = s[r] - s[l - 1];

时间复杂度分析

由于每轮询问只需要端点作差得到结果，得到前缀和需要扫描一遍，复杂度为。

差分

问题背景

给定一个长度为n的数组，给m次操作，每次操作对数组下标[l, r]的部分加c，输出修改后的数组。

暴力方法

对于每一次询问，我们都用一个for循环去为下标l到下标r之间所有的数增加c。

for (int i = l; i <= r; i++) {
    a[i] += c;
}

时间复杂度分析

同样是。

差分方法

我们引入差分数组b，b[i]表示原数组中a[i]与a[i-1]的差。 构建一维差分数组的方式：b[i]=a[i]-a[i-1]; 举个例子：a为原数组，b为差分数组

a 1 2 3 4 5
b 1 1 1 1 1

我们对数组中第二项到第四项+1，观察差分数组的变化

a 1 3 4 5 5
b 1 2 1 1 0

可以观察到b[2]加了1，b[5]减了1。 在b[2]加1，相当于对下标为2及其之后的数+1。 在b[5]减1，相当于对下标为5及其之后的数-1。 画个数轴来观察：

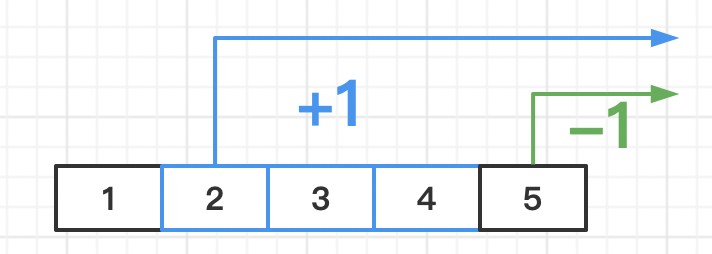
可以发现第5个数之后的部分，正负影响抵消，最终效果是范围[2, 4]内的数+1。

代码实现

#include <bits/stdc++.h>
using namespace std;

const int N = 100005;
int a[N], b[N]; // a：原数组，b：差分数组

int main(void) {
    int n, m;
    cin >> n >> m;

    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }

    // 1. 构建差分
    for (int i = 1; i <= n; i++) {
        b[i] = a[i] - a[i - 1];
    }

    // 2. 做操作
    while (m--) {  // 循环执行m次
        int l, r, c;
        cin >> l >> r >> c;
        b[l] += c;
        b[r + 1] -= c;
    }

    // 3. 对b求一次前缀和还原数组
    for (int i = 1; i <= n; i++) {
        a[i] = a[i - 1] + b[i];
        cout << a[i] << " ";
    }
    return 0;
}

这个过程有点像大家拿到一篇英文文档，先把它翻译成母语，读明白了，再给他更新做贡献，然后再翻译回英文。 翻译的过程可以借助机器，速度很快。阅读母语的效率又非常高。提高了整体的工作效率。

本题中，我们也是类似的做法，构建差分，还原前缀和都是遍历一遍的事，复杂度为，对原数组中一段的操作，改为对差分数组端点的操作，一共进行m次操作，每次操作。

时间复杂度为。