背景

我们知道BFS可以处理无权图的最短路问题，因为BFS队列扩展能够保证队列中元素距离的单调性。那本文，我们升级一下，考虑有权图的单源最短路问题。 BFS中，我们只需要拿队首元素进行扩展，在有权图最短路中，我们拿当前距离最短的点扩展就可以了。

Dijkstra朴素版

1. 设置起点的距离为0。
2. 在未确定最短路的点中找到距离最小的点t。
3. 访问t的邻接点，做松弛操作。
重复2、3两步。

#include <bits/stdc++.h>
using namespace std;

const int N = 1005;
int g[N][N];  // 邻接矩阵

bool v[N];    // v[i]:i号点的最短距离是否已经确定
int dist[N];  // dist[i]:从起点到i号点的最短路

int main(void) {
    int n, m, s;  // 点数、边数、起点编号
    cin >> n >> m >> s;

    memset(g, 0x3f, sizeof g);
    memset(dist, 0x3f, sizeof dist);

    for (int i = 1; i <= m; i++) {
        int a, b, w;
        cin >> a >> b >> w;
        g[a][b] = w;
    }

    dist[s] = 0;
    for (int i = 1; i <= n; i++) {
        int t = -1; // 存未确定的点中距离最短的点
        for (int j = 1; j <= n; j++) {
            if (!v[j] && (t == -1 || dist[j] < dist[t])) t = j;
        }
        v[t] = true; // 确定该点的最短距离
        for (int j = 1; j <= n; j++) {
            dist[j] = min(dist[j], dist[t] + g[t][j]); // 将g初始化为0x3f3f3f3f很巧妙
        }
    }

    for (int i = 1; i <= n; i++) {
        if (dist[i] == 0x3f3f3f3f) cout << -1 << " ";
        else cout << dist[i] << " ";
    }
    return 0;
}

n轮循环，每轮找到未被确定的点中距离最小的，确定它的最短路，同时更新它邻接点的距离，时间复杂度为。

Dijkstra堆优化版

上一算法中找到距离最小点的过程可以用堆优化。

#include <bits/stdc++.h>
using namespace std;

typedef pair<int, int> PII;

const int N = 2005;
vector<PII> adj[N]; // 邻接表，包括终点编号及边权

bool v[N];    // v[i]:i号点的最短距离是否已经确定
int dist[N];  // dist[i]:从起点到i号点的最短路

priority_queue<PII, vector<PII>, greater<PII>> heap; // 用距离升序，同时要保存编号

int main(void) {
    int n, m, s;
    cin >> n >> m >> s;

    memset(dist, 0x3f, sizeof dist);

    for (int i = 1; i <= m; i++) {
        int a, b, w;
        cin >> a >> b >> w;
        adj[a].push_back({b, w});
    }

    dist[s] = 0;
    heap.push({0, s});

    while (!heap.empty()) {
        int t = heap.top().second; // 拿编号
        heap.pop();

        if (v[t]) continue; // 距离小的点一定会先出堆，将v[t]标记成true
        v[t] = true;
        
        for (auto nxt : adj[t]) { // 更新t的邻接点
            int nid = nxt.first;   // 终点编号
            int nw = nxt.second;   // 边权
            if (dist[t] + nw < dist[nid]) {
                dist[nid] = dist[t] + nw;
                heap.push({dist[nid], nid}); // 允许堆中出现重复元素
            }
        }
    }

    for (int i = 1; i <= n; i++) {
        if (dist[i] == 0x3f3f3f3f) cout << -1 << " ";
        else cout << dist[i] << " ";
    }
    return 0;
}

进堆和出堆数量均为m，时间复杂度为。

Dijkstra算法对比

≈：表示在同一个数量级 朴素版用于稠密图，用邻接矩阵写。稠密图 。 堆优化版用于稀疏图，用邻接表写。稀疏图 。 若堆优化用于稠密图，则时间复杂度反而不如朴素版。 堆优化版我们允许堆中出现重复元素，而不是去修改堆的值，因为，每次堆操作是还是差异不大。

注意：当n上万时，要用邻接表写，邻接矩阵会炸内存。

Dijkstra的问题

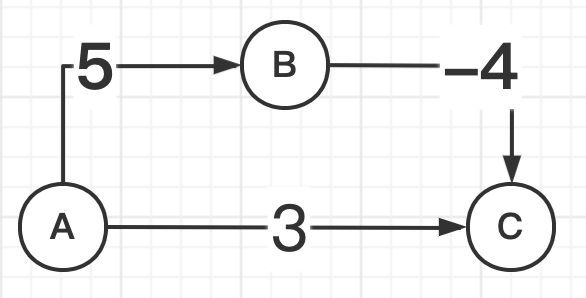
观察上图，以A为源点扩展，C的距离是3，B的距离是5。 可以确定C的最短路是3。

然而，经过A->B->C，最短路是1。

Dijkstra每次贪心地去确定距离最短的点的最短路，使它无法处理负权边。

Bellman-Ford算法

图论问题，我们经常从图的两个元素点、边入手思考。上述Dijkstra可以理解为是从点出发思考出的一类算法。下面我们介绍边出发思考的算法。

加入我们有一条边a->b，那么对这条边的松弛操作，就是看从a到b是否能让b的距离变小。

dist[b] = min(dist[a] + w[a][b], dist[b]);

如果a到d有一条最短路是a->c->b->d。这条最短路上有三条边，那么我们对所有边进行松弛操作，做3次，一定能找到这条最短路。

#include <bits/stdc++.h>
using namespace std;

const int N = 2005;
typedef pair<int, int> PII;

vector<PII> adj[N];                    // 数组，元素为vector
int dist[N];

int main(void) {
    int n, m, s;                       // 图的点数、边数、起点
    cin >> n >> m >> s;

    for (int i = 1; i <= m; i++) {
        int a, b, w;
        cin >> a >> b >> w;
        adj[a].push_back({b, w});
    }

    memset(dist, 0x3f, sizeof dist);
    dist[s] = 0;

    for (int p = 1; p <= n; p++) {                   // n轮松弛操作
        for (int cur = 1; cur <= n; cur++) {             
            for (auto nxt : adj[cur].size()) {  // 遍历所有的边
                int b = nxt.first;
                int w = nxt.second;
                dist[b] = min(dist[b], dist[cur] + w);
            }
        }
    }

    for (int i = 1; i <= n; i++) {
        if (dist[i] == 0x3f3f3f3f) cout << -1 << " ";
        else cout << dist[i] << " ";
    }

    return 0;
}

Bellman-Ford算法做松弛操作的次数决定了最短路经过的点数。如果出现了卡边数最短路问题，用该算法。 算法n次操作，每次对所有边松弛，时间复杂度为。

SPFA算法

Bellman-Ford算法有一定优化空间，每一轮用还没被访问过的点去更新其它点是无用功。我们开个队列，记录被更新的点，用队列中的点去更新别人。这就是SPFA(shortest path fast algorithm)算法。

#include <bits/stdc++.h>
using namespace std;

const int N = 2005;
typedef pair<int, int> PII;

vector<PII> adj[N];                   // 数组，元素为vector

queue<int> q;
bool inQ[N];                          // 是否在队列中
int dist[N];

int main(void) {
    int n, m, s;                      // 图的点数、边数和起点
    cin >> n >> m >> s;

    for (int i = 1; i <= m; i++) {
        int a, b, w;
        cin >> a >> b >> w;
        adj[a].push_back({b, w});
    }

    memset(dist, 0x3f, sizeof dist);
    dist[s] = 0;
    q.push(s);
    inQ[s] = true;

    while (!q.empty()) {
        int cur = q.front(); q.pop();
        inQ[cur] = false;          // 防止队列中存重复的点 

        for (auto nxt : adj[cur]) {
            int nid = nxt.first;
            int nw = nxt.second;
            if (dist[cur] + nw < dist[nid]) {
                dist[nid] = dist[cur] + nw;
                if (!inQ[nid]) {   // 队列中已经有这个点，无需再进队
                    inQ[nid] = true;
                    q.push(nid);
                }
            }
        }
    }
    
    for (int i = 1; i <= n; i++) {
        if (dist[i] == 0x3f3f3f3f) cout << -1 << " ";
        else cout << dist[i] << " ";
    }

    return 0;
}

算法对于随机数据表现较好，对于网格图，会被卡成。 如果题目中无负权边，要使用Dijkstra。

SPFA可以用于求负权回路（负环）。 若无负环，在该算法中，某个结点最多进队n次（被其它结点轮流更新一次，自己作为源点也可能入队）。 若某个结点进队超过n次，则有环。