引入

树状数组可以在O(logn)的复杂度下求区间和以及单点修改。 树状数组的作用能够完全被线段树覆盖。树状数组能解决的问题一定可以用线段树解决，反之则不然。 树状数组常数优于线段树。

线段树结构

对长度为5的区间，建立的线段树如下：

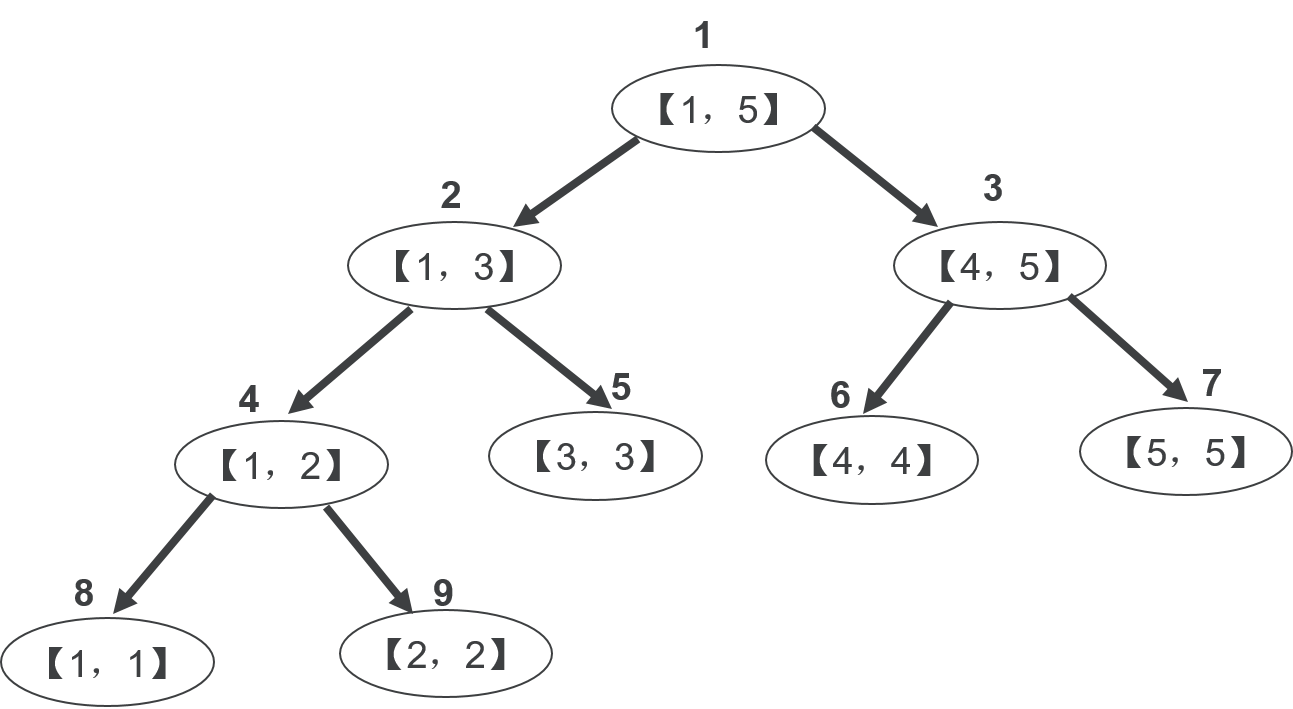
根节点就表示一整个区间，计算int mid = l + r >> 1;，将区间分为[l, mid], [mid + 1, r]两部分，即为该结点的左右孩子。

性质

1. 线段长度为N，结点数目为。 线段树中只有叶子结点()和度为2(有2个孩子, )的结点。二叉树有这样一个性质，。又因为，所以结点数目为。

对于几种操作的支持

单点修改

二分查找点的位置，沿路径修改即可。

区间查询

如上图线段树，查询区间[3, 5]元素的和，可以提取3号和5号结点的值，求和。 时间复杂度仍然是O(logn)，因为每层最多都只有两个结点包含待查询区间端点，并向下搜索。

区间修改

使用懒标记，查询用到时，再进行标记下方，类似区间查询，可同样实现O(logn)。

代码实现

可以使用动态开点，开2倍空间。 或使用堆式存储，开4倍空间。

动态开点

结点定义

const int N = 100005;
struct Node {
	int l, r;   // 区间的左右端点
	int ls, rs; // 左右孩子的编号 lson rson
	int sum;    // 区间和
};
Node node[N << 1]; // N * 2

构建函数

这里写一个构建，并进行后序遍历的例子。

// 内存池版线段树建树 2N空间
#include <bits/stdc++.h>
using namespace std;

const int N = 100005;
struct Node {
	int l, r;   // 区间的左右端点
	int ls, rs; // 左右孩子的编号 lson rson
	int sum;    // 区间和
};
Node node[N << 1]; // N * 2
int rt, cnt; // rt: 根节点编号, cnt: 内存池计数器
int n, m;
int a[N];

void build(int L, int R, int cur) {
	if (L == R) { // 递归出口
		node[cur].ls = node[cur].rs = -1;
		node[cur].l = node[cur].r = L;
		node[cur].sum = a[L];
		return;
	}
	int mid = L + R >> 1;
	node[cur].ls = cnt++; // 确定左右孩子下标
	node[cur].rs = cnt++;
	int lson = node[cur].ls;
	int rson = node[cur].rs;
	build(L, mid, lson);      // 递归构建左子树
	build(mid + 1, R, rson);  // 递归构建右子树
	node[cur].sum = node[lson].sum + node[rson].sum;  // 根节点根据左右孩子的结果，综合一下，拿到自己的结果
	node[cur].l = node[lson].l;  // 根节点的区间左端点，为左孩子的左端点
	node[cur].r = node[rson].r;  // 根节点的区间右端点，为右孩子的右端点
	return;
}

void postOrder(int root) {
	if (root == -1) return;
	postOrder(node[root].ls);
	postOrder(node[root].rs);
	cout << node[root].l << " " << node[root].r << endl;
	return;
}

int main(void) {
	cin >> n >> m;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	rt = cnt++; // cnt初始值为0，cnt++的值为0，cnt变成了1
	build(1, n, rt);

	postOrder(0);
	return 0;
}