背景

斐波那契数列：1, 1, 2, 3, 5, ... 每一个数都是前两个数的和，现在我们要求斐波那契数列的第n项。

递归

递归的一种思考方式为：你是老板，你如何分配任务。 比如说校长要统计全校有多少同学，那么只需要让每个班的班主任统计各班人数，校长做个和就可以了。

考虑老板要计算斐波那契数列第n项，它需要的是第n-1项和第n-2项，那么计算前两项的任务就交给两个小弟去处理。

写递归代码时，重点考虑两部分，递归的出口以及每层要做的事情。 在该问题下，递归的出口即是问题的已知条件，第一、第二两项均为1。

int f(int n) {
    if (n == 1 || n == 2) return 1;  // 1. 递归出口
    return f(n - 1) + f(n - 2);      // 2. 每层如何分配任务，每层要做什么事
}

递归的过程可以用一棵递归树来描述：

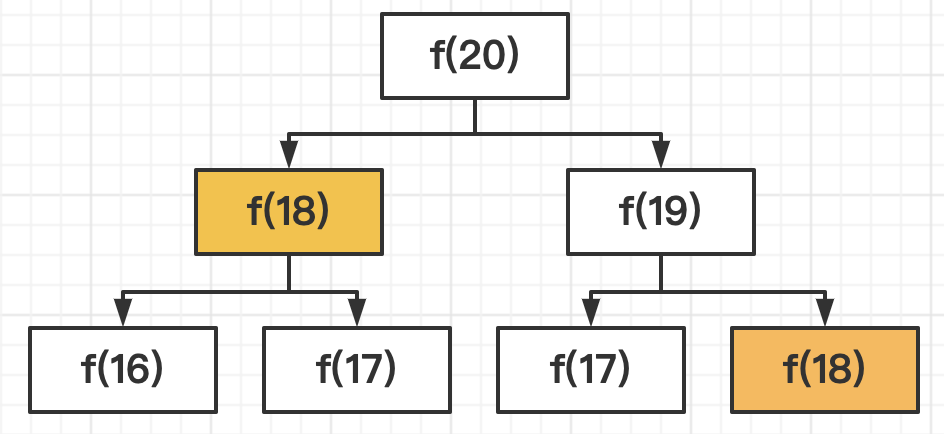
图中两个橙色的块表明f(18)被重复计算。可以想象，f(18)是一棵"参天大树"，所以普通递归写法，时间复杂度是指数级的。如何解决重复计算的问题呢？

记忆化搜索

我们可以加一个记事本，在递归的过程中，将已经计算得到的结果记录下来。这里记事本可以用数组实现

#include <bits/stdc++.h>
using namespace std;

int memo[40]; // f[i]记录斐波那契数列第i项

int f(int n) {
    if (memo[n] != 0) return memo[n]; // 记事本中存在，直接返回结果。
    memo[n] = f(n - 1) + f(n - 2);    // 将斐波那契数列的第n项记在记事本里
    return memo[n];
}

int main(void) {
    int n;
    cin >> n;
    memo[1] = memo[2] = 1; // 初始化
    cout << f(n);
}

添加记事本后，由于每一项都只会被计算一次，算法时间复杂度为O(n)，典型的用空间换时间的思路。

递推

递推的思考方式为"积跬步以成千里"，"青出于蓝而胜于蓝"的想法。从小问题出发，一步一步推出大问题的解。 我们发现，计算斐波那契数列的方式为：，画出依赖关系。

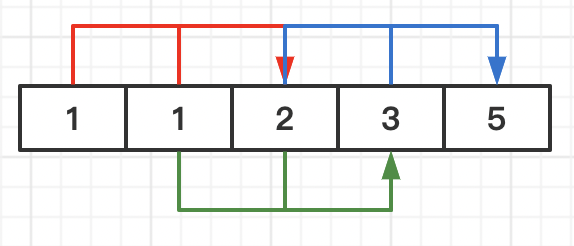
会发现它是一个有向无环图(DAG)，(如果不是DAG，就变成图论问题啦！)计算每一项都只依赖前项的结果，所以我们直接从f(1)、f(2)递推上去。

#include <bits/stdc++.h>
using namespace std;

int f[40]; // 记事本，f[i]记录斐波那契数列第i项

int main(void) {
    int n;
    cin >> n;
    f[1] = f[2] = 1;
    for (int i = 3; i <= n; i++) {
        f[i] = f[i - 1] + f[i - 2];
    }
    cout << f[n];
    return 0;
}

记忆化搜索与递推

递推这么方便，为什么还需要记忆化搜索？ 因为有些问题，计算的顺序并不那么好确定。不像斐波那契这题，直接一个for循环从小到大。 例如：滑雪